Let's increase problem level further.
Problem
Given a grid of integers L = [[A1,1, A1,2, A1,3, ..., A1,M], [A2,1, A2,1, A2,3, ..., A2,M], [A3,1, A3,2, A3,3, ..., A3,M], [..., ..., ..., ..., ...], [AN,1, AN,2, AN,3, ..., AN,M]]. Where Ai,j ≥ 0 , 0 ≤ i ≤ N, 0 ≤ j ≤ M. You have to find least perimeter of rectangle which adds up to a given integer K.
For example,
If L = [[1, 0, 0, 0, 0], [0, 0, 0, 0, 0], [1, 0, 1, 1, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 2], [1, 0, 0, 0, 0]] and K = 3 , The answer would be 22, rectangles will be {(2, 3), (4, 4)}.
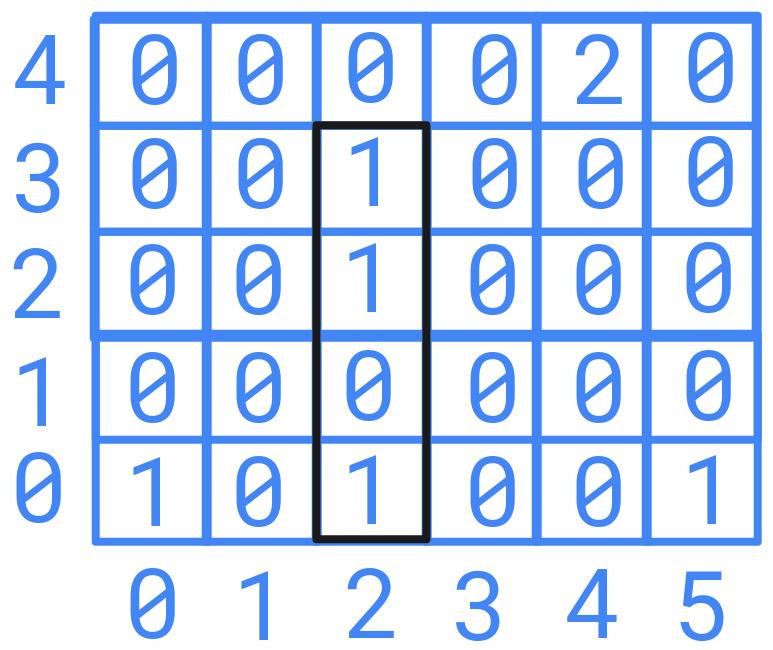
Solution
The first approach that comes to mind is calculating 2D prefix sum, and then finding least perimeter rectangular field adding up to K.
Calculating 2D prefix sum will take \(\cal{O}(N \cdot M)\) time. But, if we find rectangle adding up to K by taking every possible rectangle then it will take \(\cal{O}(X)\) time, where X = Number of possible rectangles. Let's calculate X. We will choose two indices of length, and two vertices of width, which will form a rectangle. Number of ways to choose two indices of length is \(N \choose 2\) and of width is \(M \choose 2\).
$$X = {N \choose 2} \cdot {M \choose 2}$$ $$= \frac{N\cdot(N+1)}{2} \cdot \frac{M\cdot(M+1)}{2}$$ $$= \frac{(N^2 + N)\cdot(M^2 + M)}{4}$$ $$X = \frac{N^2 \cdot M^2+N^2 \cdot M+M^2 \cdot N+M \cdot N}{4}$$
We can see that overall time complexity is \(\cal{O}(N^2 \cdot M^2).\) Can we optimize it? ...Yes, by using sliding window algorithm on 2D array. But, how we will apply sliding window algorithm on a 2D array?
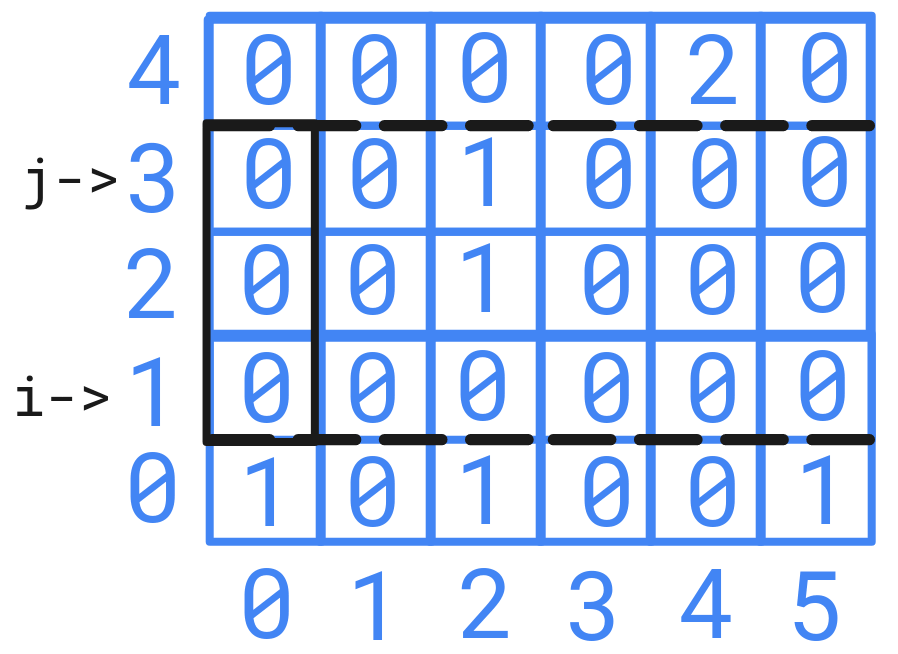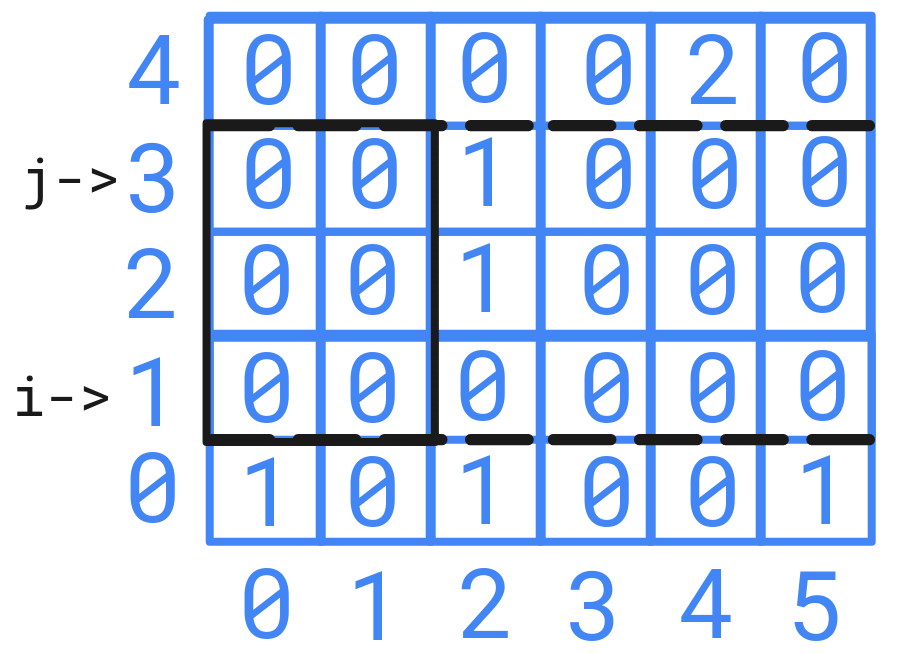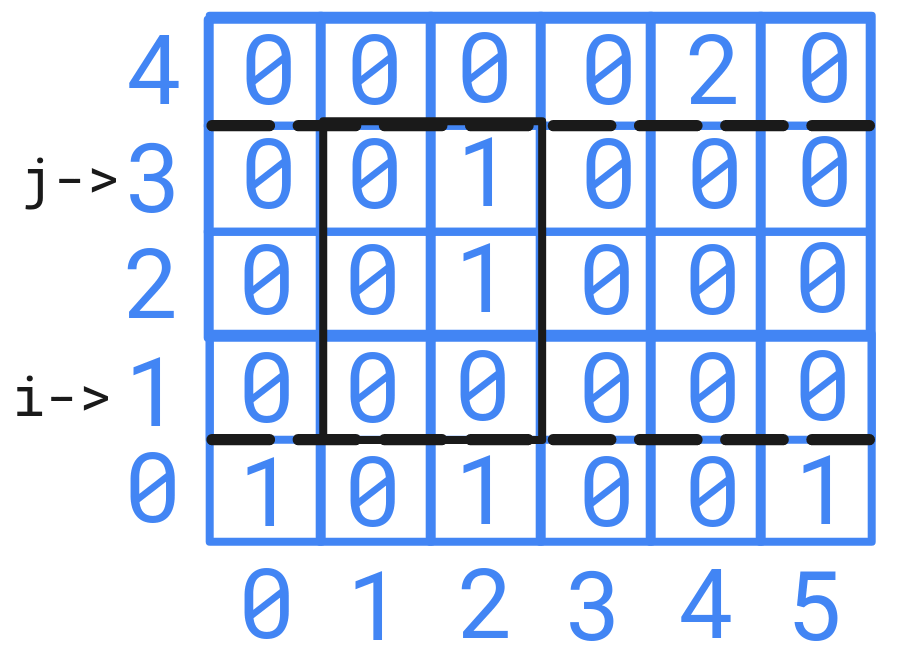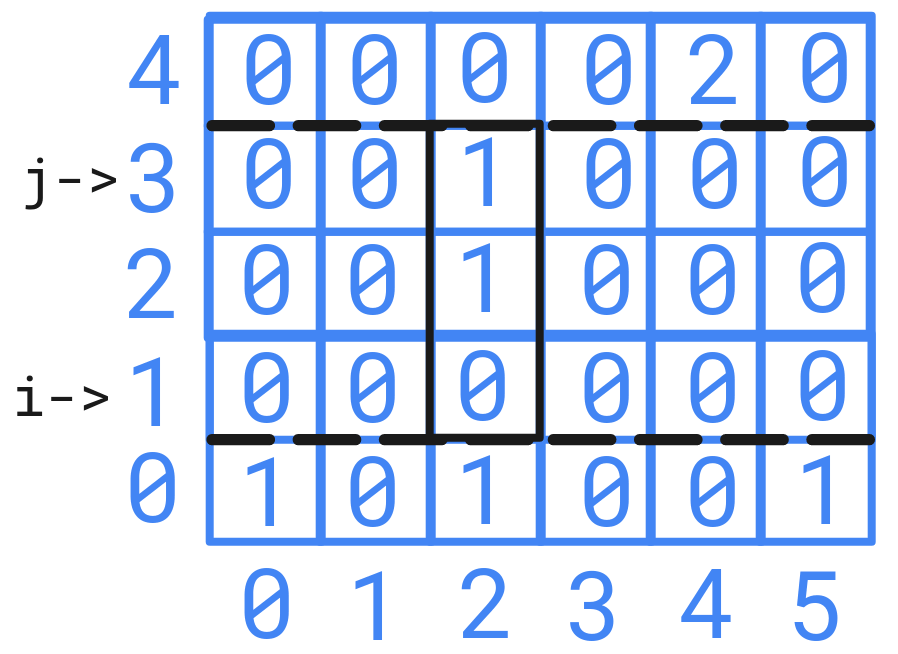
For using sliding window algorithm, we have choose two indices from either row or column as shown below and apply sliding window with fixed row or column.
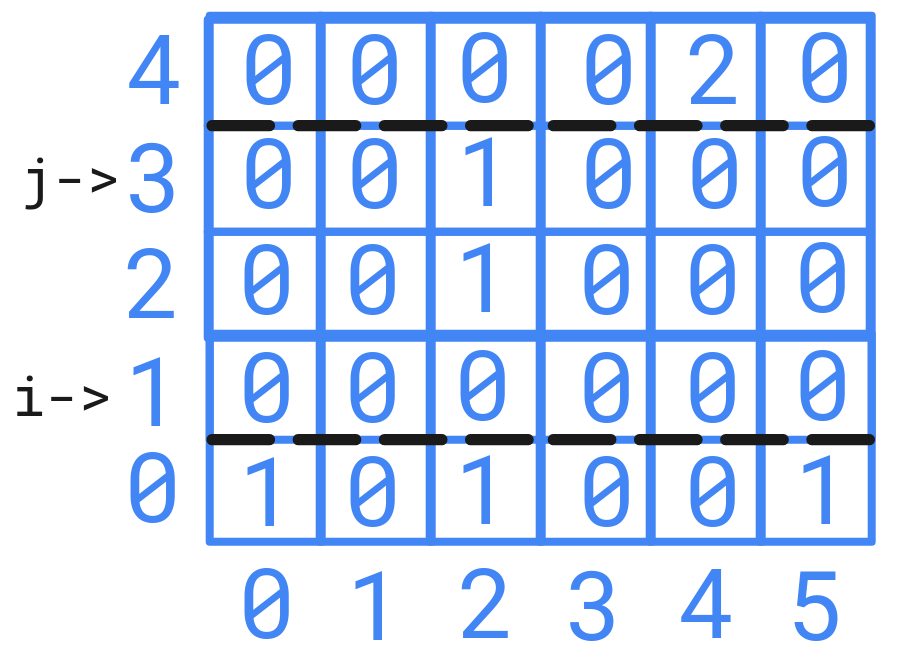
Using sliding window for a fixed rows or columns will take \(\cal{O}(N)\) or \(\cal{O}(M)\) time complexity accordingly. As we have to repeat it for others fixed rows or columns also. Which will result in \(\cal{O}(N \cdot M^2)\) or \(\cal{O}(M \cdot N^2)\) time complexity.
Code
Problem : Garden, 2005
Question summary:
A rose garden in rectangular form is l meters long and w meters wide. We have to fence two rectangular fence inside the garden such that both are disjoint and sum of their perimeter is minimal. So, we have to just output sum of perimeter of those rectangles.
Solution
We will divide the rectangle vertically and find both side rectangle with minimum perimeter. Doing this will ensure that rectangles are disjoint. Repeat the process now by dividing rectangle horizontally. We have already discussed the process to find the rectangles with sum equals to K. So, how exactly we are going to find the minimium perimeter rectangle within the range?
To find minimum perimeter rectangle in the range, we will have to take four array, two of size N (for rows) and two of size M (for columns).